In the last part of Bits & Beyond, we talked about cryptology of data. In this part, we will talk about how data is encoded in order to compress data, about information systems and about the internet. Let's start
General encoding
When data is encoded, it is converted into another information language. For example:
Binary numbers
Binary numbers are numbers in the dual system. The dual system is a place value system with the basis of 2, that means it only has two numbers (0 and 1), differently from the decimal system, which has the basis 10, which means it has 10 numbers (0 to 9).
Of course, it is possible to convert decimal numbers into binary numbers. Let's take a look at that.
Converting decimal numbers into binary numbers
There are two ways to do that.
The residual procedure
The into binary numbers converted decimal number is divided by 2. The calculation results in a whole number and a rest. The rest is noted separately.
The whole number of the previous calculation is divided and, again, the result is a whole number and a rest. You repeat this step, until the result of the division is 0.
Now, you write each rest one another and read it from bottom to top or from right to left, That is the binary number of the decimal number.
Let's take a look at an example:
Number = 42
Legend: R = rest
1. 42 / 2 = 21 R: 0
2. 21 / 2 = 10 R: 1
3. 10 / 2 = 5 R: 0
4. 5 / 2 = 2 R: 1
5. 2 / 2 = 1 R: 0
6. 1 / 2 = 0 R: 1
From bottom to top: 101010
The binary number of 42 is 101010.
Place value method
You determine the power of two, which result is either equal to the decimal number or the next lower number to it. This will be subtracted from the decimal number
You determine the power of two, which result is either equal to the result of 2.1 or the next lower number to it. This will be subtracted from the result of 1. You repeat this step until the difference results in 0.
The binary number is obtained by adding 1 (starting with the highest exponent) to the places represented by the exponent and writing 1 to any of these places for which a power of two exists.
This might be complex to understand, so let's take a look at an example:
Number = 45
Next lower power of two to 45 = 2^5 (32)
> 45 - 32 = 13
Next lower power of two to 13 = 2^3 (8)
> 13 - 8 = 5
Next lower power of two to 5 = 2^2 (4)
> 5 - 4 = 1
Next lower power of two to 1 = 2^0 (1)
> 1 - 1 = 0
>> 2^5 2^3 2^2 2^0
>> 1 is at place 5+1 and 3+1 and 2+1 and 0+1, the rest is 0
>> Place: 6 5 4 3 2 1
>> Number: 1 0 1 1 0 1
You could also use the index instead calculating the places
>> Index: 5 4 3 2 1 0
>> Number: 1 0 1 1 0 1
You can of course also convert binary numbers into decimal number. Here's how.
Converting binary numbers into decimal numbers
The general equation is: x * 2 ^ (n-1) + ... + x * 2 ^ (1 - 1).
Here, x is the number at place n, n is the length of the number chain.
Let's take a look at an example:
Binary = 1011
1 * 2^(4-1) + 0 * 2^(3-1) + 1 * 2^(2-1) + 1 * 2^(1-1)
> 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0
> 8 + 0 + 2 + 1
> 9
ASCII
The ASCII-Code is a set of character to present texts in computers. Every control character and printable character has a unique numerical code. The binary code is by default a 7-bit-code but was increased to an 8-bit-code.
If you're interested, take a look at this website. Here you can find an ASCII-table.
RGB-Model
Most displays use an RGB-model, which means that every color on a display is a mix of red, green and blue. The amount of proportion, every color has in a color can be indicated by hexadecimal numbers.
The color yellow can be created, by giving the maximum amount of red and green proportions and the minimum of blue proportions. That would be RGB (255, 255, 0). In hexadecimal, you would write #FFFF00. The contrast black can be created by removing any color proportions, so RGB (0, 0, 0), which would be #000000 in hexadecimal, and the contrast white can be created by giving the maximum amount of each color proportion, so RGB (255, 255, 255), which would be #FFFFFF in hexadecimal.
But encoding is not just to represent information, it is also to compress data, for example words.
Encoding to compress
Huffman coding
Usually, each character in a word takes 8 bits, since each character of the ASCII-Code is 8 bits long. For a word like "Mississippi", that would 88 bits. A sentence like "The Mississippi River is the primary river, and second-longest river, of the largest drainage basin in the United States" would already take 912 bits (if I calculated that correctly). The Huffman-coding makes it possible to compromise the bits a word would take.
In the Hoffman coding, the most present character should take the least amount of bits. The characters are coded in binary codes, but the binary code is variable. That means, for every different string, there would be another binary code.
The Huffman-code fulfills the so-called Fano-condition, that means no code word is the beginning of another code word, so the code is uniformly decodable.
The algorithm of a Huffman-Code runs through a so-called Huffman-tree. This is built as follows:
The different characters of a string are counted
The both characters, that are present the least, are connected by a node. In this node, the sum of their occurrences is written down.
For that:2.1. The character, that occurs more often of these twos, is written in the right leaf.
2.2. If both characters occur equally often, it can be decided individually
The second step is repeated until all characters are existing as nodes or leafs in the Huffman-tree.
The nodes are connected by a line. On the left line, you can either write a 0, or remember that the left line equals 0 and on the right line, you can write a 1 or remember that the right line equals 1.
From the root of the tree, you are reading the value of the line until you are at the leaf of the needed character.
At the end, you get a chain of binary numbers, that represents the word.
We can use our example word "Mississippi" to showcase this.
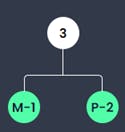
The character M and the character P are existing least of all characters. M exists least often than P, thus it is written in the left leaf.
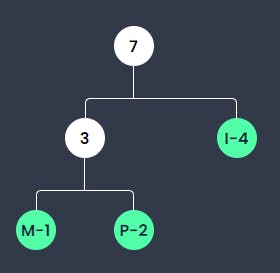
I exists more often than the sum of M and P together, thus it is written in the left leaf. Together, the sum is 7, which is written in their node.
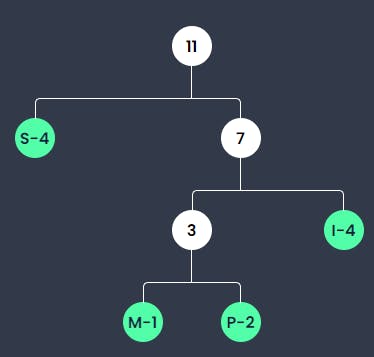
S exists 4 times and thus is smaller than the existence of I and the sum of M and P. Therefore, it is written in the left leaf.
If we now want to get the compromised version of Mississippi, we get it as follows:
M = right(1) > left(0) > left(0) = 100
I = right(1) > right(1) = 11
S = left(0) = 0
p = right(1) > left(0) > right(1) = 101
That results in 100 11 0 0 11 0 0 101 101 11
As a string, Mississippi uses 88 bits. By coding it with the Huffman coding, we only use 21 bits.
Run-length encoding
The run-length encoding is a loss-free compression-algorithm, that is good for compromising multiple repetitions.
Instead of writing the repeated character over and over again, only the numbers of repetitions, followed by the repeated character, is written down. For example:
Example = AAAAA BBBBBBB CC DDDD (144 bits)
Encoded with RLE: 5A 7B 2C 4D (64 bits)
Problems
The RLE should only be used, when there is a big amount of repetitions, as it could also end up using more bits than the word that should be compromised.
Example = M i ss i ss i pp i (88 bits)
Encoded with RLE: 1M 1i 2s 1i 2s 1i 2p 1i (128 bits)
Now, you have learned about encoding and should have a basic understanding of what encoding is and how it works, as well as how it can be used to compromise data.

