Table of contents
Last time, we learned about the basics of data structures. In this entry of Bits & Beyond, we will learn about binary trees. Binary trees are a part of data structures but given its amount of information, you have to learn, I decided to make an extra entry for it.
So, without any further hold-backs, let's start!
Binary search
Before we can learn about binary trees, let us quickly introduce binary search, which might help us to understand, why binary trees are build like this.
So, imagine you have a list of numbers, like this:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
and you want to find a specific number, let's say 9.
With a simple search algorithm, you might start from one end of the list and check each number until you find the one you're looking for. This could take a long time, especially for large lists.
But with binary search, you can find the number much faster. Here's how it works:
Start in the middle: Instead of starting from one end, you start in the middle of the list. So, you check the number in the middle of the list, which here is 6.
Compare: Now, you compare the number you're looking for (9) with the number in the middle of the list(6).
Three possibilities:
If the number you're looking for is equal to the middle number, you found it!
If the number you're looking for is greater than the middle number, you can ignore the left half of the list and focus on the right half.
If the number you're looking for is smaller than the middle number, you can ignore the right half of the list and focus on the left half.
Repeat: Now, you repeat this process with the remaining half of the list. You keep dividing the list in half and checking the middle number until you find the number you're looking for.
In our example, you'd next check the middle number of the right half (7, 8, 9, 10, 11), which is 9, and you've found the number you were searching for!
So instead of checking each number one by one, binary search helps you narrow down your search much faster by dividing the search space in half each time. This makes it a very efficient way to find items in a sorted list.
Binary trees use a similar idea of dividing a search space efficiently, but they're structured in a tree-like format, which can have various applications in computer science, from organizing data efficiently to optimizing search algorithms.
Binary trees
Binary trees consist of a root and a finite number of nodes.
Root: This is the topmost node in the tree. It serves as the starting point for any traversal or search operation within the tree.
Nodes: Each node in the binary tree contains a piece of data and may have references (pointers) to its left and right children, if they exist.
Children: Every node can have zero, one, or two children. If a node has children, they are typically arranged in such that the left child (if it exists) holds a value smaller than the parent node, while the right child (if it exists) holds a value greater than the parent node.
Parent node: Except for the root node, every node in the binary tree has exactly one parent node, which is the node directly above it in the hierarchy.
Leaf: If a node has no right or left child, it is called a leaf.
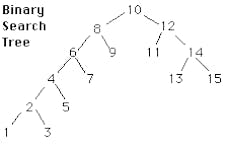
As can be seen in the image, the structure is quite simple.
Every left child (and their children) has to be smaller than its parent.
Every right child (and their children) has to be greater than its parent.
Traversal of binary trees
Traversal means the systematic investigation of nodes of a tree in a certain order. For this topic, we use the following binary tree:
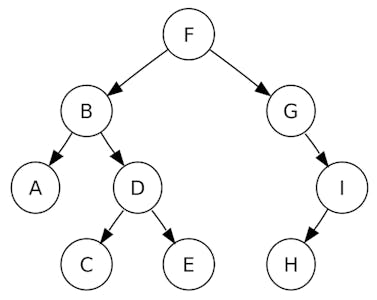
There are three possible traversals:
InOrder: Following the InOrder traversal, you start from the leftmost node A, then move up to its parent B, then to the leftmost node of the right subtree C, back to its parent D, then its right child E, and so on, until you reach the last node I.
The result of this traversal on this tree would be: A, B, C, D, E, F, G, H, I.
PreOrder: In PreOrder traversal, you visit the current node before its children. Starting from the root node F, you visit it first, then move to its left child B, then its left child A, and so on, until you reach the leftmost node of the tree. After that, you backtrack to the parent node and visit its right child, if it exists. This process continues until all nodes are visited.
The result of this traversal would be: F, B, A, D, C, E, G, I, H
PostOrder: Following the PostOrder traversal, you visit the current node, after visiting its children. Starting from the leftmost leaf node A, you move to its parent B, then to its right subtree, visiting C and E before visiting D. After visiting all nodes in the left subtree of B, you backtrack to B and then move to its right subtree, visiting H before visiting I. Finally, you visit the root node F.
The result of the traversal would be: A, C, E, D, B, H, I, G, F
Now you should have gotten a basic understanding of what binary trees are and how they work.

